Finding the composition of the function f with the function g :
g(x) is in the domain of f, making it an input.
f of g of x
Find f(g(x)) when f(x) = 2x + 5, and g(x) = x - 6
The first step: Understanding what the problem is asking is important when solving. Instead of plugging in x for f(x) , you are now using the function g(x). It becomes your new input.
Solving:
f(g(x)) = f(x - 6)
= 2(x-6) + 5
= 2x - 12 +5
Evaluating f(g(x)) when x has a specific value such as 1 or 2 is simple now that we already found f(g(x)).
When x = 1, you simply plug that number in 2x - 7, which gives you an answer of -5.
g of f of x
g(f(x)) consists of the same methods of solving as f(g(x)), because f and g are still both just functions.
g(f(x)) = g(2x + 5)
= 2x + 5 - 6
= 2x - 1
As you can see, g(f(x)) ≠ f(g(x)) in this case, but sometimes they are equivalent.
Video: http://www.youtube.com/watch?v=S4AEZElTPDo (This video explains all the concepts I went over about the composition of two functions clearly.)
Identifying Functions
As well as the composition of functions, there is also identifying functions. The function h is an example used to identify two functions.
For example if h = (2x-7)³, then for f(g(x)), f = x³ and g = 2x-7
Finding the inner and outer functions is the whole concept of identifying them. f is the outer while g is the inner.
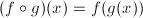.gif)

.gif)
.gif)
.gif)
No comments:
Post a Comment