All functions are written in function notation, where f(x) will equal something.
Example: f(x) = 2x +1
If you were to graph this function, f(x) would just be the y coordinate, or the output value, of the function from the input of x. Just replace f(x) with y:
y = 2x + 1
When you are looking for the inverse of a function, what you are really doing is undoing all of the operations done to x. When finding the inverse, the same as before will be done by replacing f(x) with y. To undo the operations to x, simply switch the variables x and y (or if there is more than one x, replace each with a y):
x = 2y + 1
Now, solve for y:
x - 1 = 2y
This answer is correct, however, to write the inverse of a function in correct function notation, substitute y for 

Final Answer:
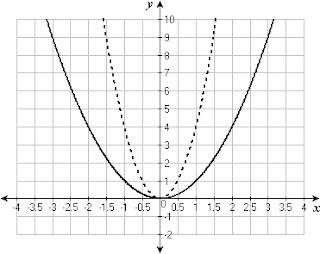
Here are two examples of graphs of functions and their inverses:
Here is a short video that shows the same steps but to a longer function:
The big point to remember is to switch your x and y values and then solve for x. Be sure to check if your inverse is actually a function because it is possible that one does not exist!
Hope this helps! -Sofia

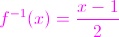

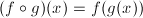.gif)

.gif)
.gif)
.gif)