Transformations of Functions (1.3)

Transformations of Functions (1.3)


Hey, I will be reviewing the transformations of functions. 

Lets get right to it, its not too difficult but a friendly tip, if the transforming factor added, like a number or fraction etc., to your function is inside of your parenthesis you basically take the opposite of what it should be (multiply by -1).


Translation (Movement)

Outside the parenthesis
For example if we have f(x)+2 the function will move UP 2 units.
If we have f(x)-2 then it will move DOWN 2 units, very logical.

Then we move into the parenthesis...
f(x-2) this will move the function over RIGHT 2 units, not left as you may think.
f(x+2) this follows the trend and will move the function 2 units LEFT.

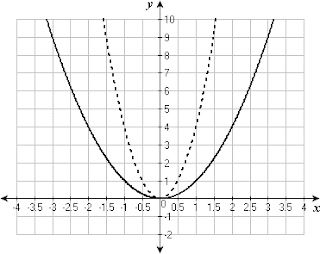
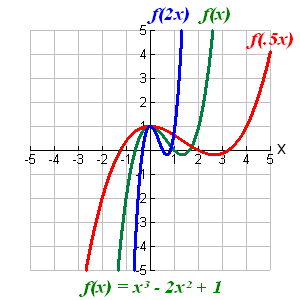
Stretching

This is where it affects the actual appearance of your graph but hods your intercepts. 

c is any number

f(x) c      This makes your function steeper, but holds all x intercepts in place. Acts like it should, smaller makes the function smaller.

f(x c)       This stretches your function horizontally making a smoother incline and holds all mins and max's in                place as well as the y intercept. acts opposite than you think making less than 1 stretch the function.

Reflecting

Once again 2 types; in and out of parenthesis...

-f(x)    Reflects over the x-axis

f(-x)    Reflects over the y-axis

Those are the transformations of functions, and I hope the graphics help you remember what is what.

Just remember, if it's in the parenthesis, it acts opposite of common sense.

Good luck, Tyler.