Chapter 4 Review

Radian Measures:

When measuring an angle (either in degrees or radians) you have an initial side and a terminal side. Finding a coterminal angle is when both angles have the SAME terminal side. The figure 1.1 bellow shows what a terminal side it. Figure 1.2 shows an example of a coterminal angle

1.1                                                           1.2

Radian & Degree Conversions:

When converting between radians and degrees we use the formulas:

Examples: 

                    

 To convert degrees to radians; you divide by 180 degrees and multiple by pie. This process allows for the degrees to cancel out, leaving only radians present.

To convert radians to degrees; you divide by pie units and multiple by 180 degrees. This allows for the units of pie to cancel out, leaving only degrees present.

Arc Length:

When wanting to calculate the arch length of a circle we use the formula:

* This equation can only be used when Theta is in radians!!!

Trig Functions (When looking at unit circle):

Trig Functions (When looking at triangles):

    

 

Pythagorean Identities:  







Reference Angles: 

As shown bellow in the red, reference angles are the smaller angles that are formed from the terminal side of the original angle. Reference angles allow us to use an easier angle than that of the original angle. When angles are greater than 90 or 180 degrees reference angles are used. 

Graphs of: Sine, Cosine, and Tangent functions:

Phase shifts: 

Adding or subtracting of some degrees inside the the angle, changing the angle causes the whole graph to either shift left (if addition) or right (is subtraction).

Adding or subtracting of some degrees outside of the angle, causes the whole graph to either shift up (is positive) or down (if negative).

Graphing Cosine functions:

  The amplitude of the cosine graph shown is 1. This is due to the fact that each peak and trough is 1 unit from the divider (middle) of the graph. 

   To find the period of the cosine graph we use the equation: 

Graphing sine functions:

   The amplitude of the sine graph bellow is 1. This is due to the fact that each peak and trough is 1 unit from the divider(middle) of the graph, much like the cosine function. 

   To fine the period of the sine graph we use the equation: The same as the cosine graph.

Graphing tangent functions:


Because Tan= sin/cos we are able to determine the tangent graph. The tangent function vertical asymptotes' lay where 'x' intercepts of the cosine function are. We can determine that they are a vertical asymptotes from previous chapters we determined the vertical asymptotes by setting the denominator equal to zero (or when cosine equals zero).
  The period of a tangent function is:

The amplitude of a tangent function is undefined because it is a tangent function.

Graphs of: Sec, Csc, and Cotangent functions:

  

   Graphing cosecant functions:

To graph the cosecant functions you can first look at the graph of the sine function. The cosecant function starts at the peaks and troughs of the sine functions. The csc function has vertical asymptotes when the sine function at the x intercepts. The vertical asymptotes create the csc graph to continue upward and downward towards positive and negative infinity. 

Graphing cotangent functions:
  When graphing cotangent functions you use all the same tools as when you graph tangent functions. the only thing that changes is that the graph will begin to raise on the right to left, instead of left to right.

 Graphing secant functions:
    When graphing secant function you begin the the parent function of a cosine graph. You take all the peaks and troughs on the cosine graph and that is where you begin you secant graph, (at the highest point). The secant graph will have vertical asymptotes where the cosine function crosses the x axis. 

Graphing Inverse functions:

Graphing Inverse Sine functions:

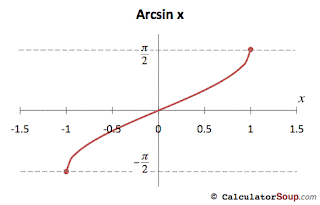  When graphing an inverse sine function you can only take a small amount of the graph, this is due to the horizontal line test. Because the function doest pass the horizontal line test in the parent function is will not pass the vertical line test unless you cut down part of the graph in the beginning. We want to take the graph of the sine function from negative pie/2 to positive pie/2.

 Graphing Inverse Cosine functions:
    When graphing an inverse cosine function you can only take a small amount of the graph as well. This is also due to the fact that the inverse function wouldn't be fa function because the whole cosine graph is not one to one, only a small part of it is. 
    When graphing the inverse cosine function we want to take from zero to positive pie. 

Graphing Inverse Tangent functions:

    When graphing an inverse tangent function you can only take a small portion of the graph. Like the inverse sine function we will only take a part of the graph from negative pie/2 to positive pie/2. Because he tangent graphs normally have vertical asymptotes they will be horizontal asymptotes once you flip all the x and y coordinates.